在计算机科学与数学领域中，NP完全问题是一个十分复杂且充满神秘色彩的主题。自二十世纪七十年代以来，它便成为了理论计算机科学与算法研究领域中极为重要的研究课题之一。NP完全问题不仅揭示了多项式时间内可解问题与NP类问题之间的界限，还促使了诸如P=NP问题等更为广泛的问题的产生，从而成为了推动计算机科学发展的重要动力之一。

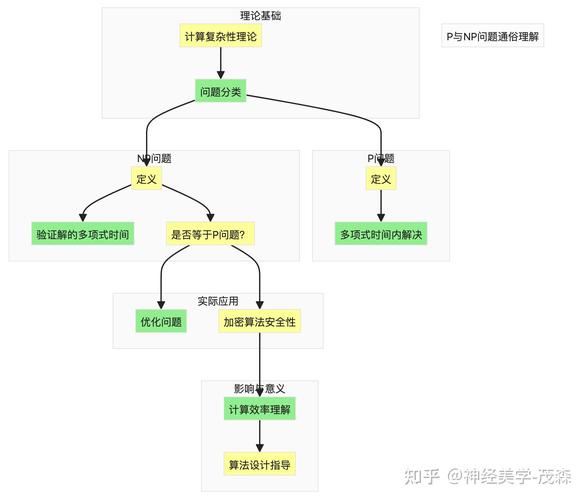
NP完全问题，全称为Nondeterministic Polynomial，即非确定性多项式时间问题。这类问题是一类在非确定性多项式时间内可解的问题，即可以通过非确定性图灵机在多项式时间内找到一个解。然而，NP完全问题也具有一个重要的特性，即对于这类问题，若能够在一个输入实例中找到任何一个解，便可以在多项式时间内验证这个解是否正确。因此，NP完全问题可以看作是NP类问题中一个重要的子集，而P=NP问题则是决定NP完全问题是否可以在多项式时间内求解的一个核心问题。NP完全问题的定义与性质，为研究这些问题的算法复杂性提供了重要的理论基础。同时，NP完全问题在现实世界中的许多实际问题上也具有着广泛的应用前景，因此成为了理论计算机科学中的重要研究方向之一。

NP问题的研究，可以追溯到二十世纪六十年代末和七十年代初。1971年，斯蒂芬·库克（Stephen Cook）在《计算复杂性的理论》这一著名论文中首先提出了NP完全问题的概念。他证明了布尔等式可满足性问题（SAT）是NP完全问题，并提出了著名的Cook-Levin定理。自此之后，NP完全问题迅速成为了计算机科学与算法研究领域中的重要研究方向。1972年，理查德·卡普（Richard Karp）通过列举并证明了21个经典问题属于NP完全问题，进一步推动了NP完全问题的研究与发展。自此以后，对NP完全问题的研究逐渐成为理论计算机科学中的一个核心方向。

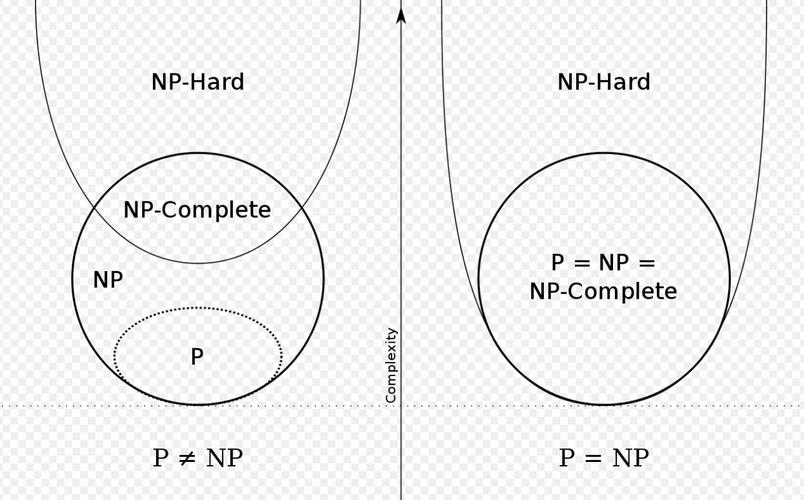
NP完全问题的一个重要特征是它们之间存在着多项式时间归约的关系。如果一个NP完全问题可以通过多项式时间归约转换为另一个NP完全问题，那么这两个问题在复杂度上是等价的。因此，在研究NP完全问题时，我们可以通过寻找一种多项式时间归约来证明两个问题在复杂度上的等价性。这一特性使得NP完全问题间的互相转换变得尤为重要，也成为了NP完全问题研究中的一种重要工具和方法。通过这种转换，研究者可以将一些较为复杂的NP完全问题转化为更为简单或熟悉的问题，从而更好地理解这些问题的性质以及寻找可能的算法解决方案。

NP完全问题的研究对于实际应用具有深远的影响。一方面，NP完全问题的研究促进了计算机科学与数学理论的发展。通过研究NP完全问题，人们可以更深入地理解算法复杂性，并推动了计算复杂性理论的发展。另一方面，NP完全问题的研究也对实际问题的解决产生了积极的影响。许多实际问题，如旅行商问题、背包问题等，都可以被归类为NP完全问题。通过研究这些问题，人们可以更好地理解这些问题的复杂性，并进而开发出更为有效的近似算法和启发式算法，以求得这些问题的近似最优解。此外，NP完全问题的研究还推动了算法设计与分析方法的发展，为解决实际问题提供了重要的理论指导。

NP完全问题的研究仍然存在许多挑战与难题。首先，尽管NP完全问题已经被广泛研究，并且已经证明了许多经典问题是NP完全问题，但P=NP问题仍然悬而未决，成为计算机科学领域中最大的未解之谜之一。其次，对于NP完全问题，目前还没有找到能在多项式时间内求解的算法，因此对于这些问题的求解，通常只能采用近似算法或启发式算法。此外，研究NP完全问题还需要解决许多复杂性理论方面的难题，如归约方法的改进、NP完全问题的分类等。这些问题的存在，也使得NP完全问题的研究成为一个充满挑战与困难的研究方向。

总之，NP完全问题作为计算机科学与数学领域中的重要研究方向之一，不仅揭示了多项式时间内可解问题与NP类问题之间的界限，还对于实际问题的解决具有重要的理论指导意义。尽管NP完全问题的研究还存在许多挑战与难题，但通过不断的研究与探索，我们相信这些问题最终将被解决，从而推动理论计算机科学与算法研究的发展。